Quantum-Mechanical Theory of Molecular Polarizabilities
| Return to Quantum Mechanical and Perturbation Theory Menu | Next Topic |
Quantum-Mechanical Theory of Molecular Polarizabilities up to Third Order
The literature refers to first order, second order and third order polarizabilities. You may also see “first order hyperpolarizability “ which is the same thing as second order polarizability. These conventions may be confusing.
Our goal is to be able to relate the chemical structure and the nature of the pi-conjugated backbone, and the nature of donor and acceptors to the to kind of non-linear response that can be measured or calculated.
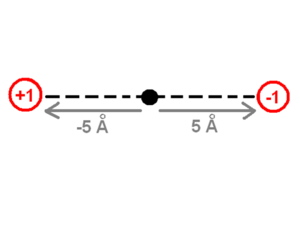
The expression for dipole moment is simply the sum of all the point charges over all those point charges of the charge itself times the position of that charge.
Dipole moment
The drawing of the charges shows a point charge of +1 on the left side and a point charge of -1 on the right side. The origin of the system of coordinates is in the middle of these charges. The point charge of +1 is -5 angstrom away from the origin and the point charge of -1 is +5 Ångström away on the x-axis. The first step to calculate the dipole moment is to multiply the charge +1 by the position -5 Angstrom for the +1 point charge, which will be -5eA (electron times angstrom). Then do the same for the -1 point charge (-1 * 5) which equals -5eA as well. Finally the sum of these values (-5eA + -5eA) -10eA, which corresponds to about -48 debyes, will be the dipole moment. The literature does not use the SI units of the dipole moment because the SI units use coulomb for the charge and meters for the distance which are macroscopic units. Instead, the dipole moment units use electron units and Angstrom (eA), or Debye.
- <math>Cb \cdot \, m \, or Debye \approx 4.8 q(\vert e \vert) * d( A )\,\!</math>
If there is a donor acceptor compound, a full charge transfer can occur. The drawing shows the two point charges that are 10 angstrom apart with the length of the conjugated bridge between them. Then with one full electron charge transfer across 10 angstrom, a dipole moment of 50 debyes will be obtained (this is quite large). If the donor and acceptor are about 10 angstrom apart and the dipole moment is about 10 debyes, the system has a charge transfer of about 0.2 electrons from the donor to the acceptor assuming it a simple dipole.
This example is a simplified model where the origin of the system of coordinates was placed midway between the two charges. However, what would happen if the origin of the coordinates is placed on the +1 point charge? What will be the dipole moment? To answer this question, the +1 point charge will be multiplied by a distance of 0 (due to the origin of the coordinates) and that will not contribute anything to the dipole moment. The -1 point charge is now at a distance of 10 angstroms away and is multiplied by a charge of -1 which is -10 eA or about -50 debyes (-48 precisely). Consider the case where the molecule is not neutral but instead a cation is formed with a +2 charge on the left. If the origin of the system of the coordinates is at the +2 point charge, the calculated dipole moment will be -10 eA. But if the origin of system coordinate is placed on the -1 point charge, the dipole moment will be -20 eA. An important lesson out of these examples is that with a charged system, the dipole moment depends the choice of origin of coordinates. The dipole moment is no longer perfectly defined.
In the previous example in which the point origin of coordinates was placed on the +1 point charge, there was a net charge so the monopole is not 0. Therefore, the dipole and all the other poles (quadrapole, octapol, hexapole etc.) depend on the origin of the system of coordinates. However, if the monopole is 0, then the dipole doesn’t depend on the origin of coordinates. But if the dipole is not 0, which means there is a permanent dipole moment in the molecule, then the dipole and the other poles will depend on the origin of coordinates. If the monopole is 0 and the dipole is 0, due to the central symmetric molecule, then the quadrapole will not depend on the choice of the origin of the system of coordinates. It is only when the molecule doesn’t carry a net charge that the dipole is really defined. Otherwise, if the molecule does carry a net charge, the dipole is not defined and it will depend on the origin of the system of coordinates that is chosen. This also creates further complications as it is important to make sure that the point of references is the same for similar systems in order to make comparisons. But for now, when one talks about dipoles, the dipoles will be from neutral molecules so that there will be no complications. In the case of two photon absorption molecules the quadrupole moments can be important. But since these molecules are usually centro symmetric and the dipole is 0, the quadrapole will not depend on the choice of the origin of the system of coordinates.
In the case of point charges where it is easy to describe the degree of dependencies or on the system of coordinates.
- <math>\overrightarrow{\mu} = \sum_i q_i \overrightarrow{r_i}\,\!</math> is the dipole for point charges
But if we have a molecule, the Heisenberg principle does not allow a precise location of the electron. Therefore, wave functions are needed. To get the dipole moment, it is necessary to look at the electronic densities at a given point in space. The expression consists of a wave function at a given point in space r (in other words, wave function at r) and the dipole operator. The dipole operator is the electronic charge of the particles being discussed multiplied by the position of those charges. Since r doesn’t modify Ψ, the Ψ can be arranged so that a psi squared is obtained, which is an electronic density. This makes sense because the wave function squared is an electronic density, and so the expression is equal to an electron density multiplied by a position. Those two expressions are perfectly consistent with one another.
- <math>\overrightarrow{\mu} = \int_{-\infty}^{\infty} \Psi^* e \overrightarrow{r} \Psi d \overrightarrow{r}\,\!</math> is the dipole for a molecule
where
- <math>\Psi^*\,\!</math> is the wave function for position r
- <math>e \overrightarrow{r}\,\!</math> is the dipole operator relating the charge and position of charges.
- <math>\langle \Psi \vert \overrightarrow{r} \vert \Psi \rangle\,\!</math> determines the dipole moment in the state described by the wave function Ψ
- <math>\overrightarrow{\mu}_g = \langle \Psi_g \vert \overrightarrow{r} \vert \Psi_g \rangle\,\!</math> This is just the Dirac expression for this integral expression.
The dipole moment can be examined at the excited state and this is critical for second order materials. To find the dipole moment in the excited state S1 of organic chromaphore, use the wave function of that particular excited state.
Transition Dipole
The dipole moment should not be confused with the transition dipole in which describes the transition from a given state to another state. Usually it is the transition from ground state to an excited state. In that case, the wave function psi g will be that of the initial state and the wave function psi e will be that of the final state.
- <math>\overrightarrow{\mu}_{eg} = \langle \Psi_e | e \overrightarrow {r} | \Psi)g \rangle\,\!</math> the transition dipole
- <math>\overrightarrow{\mu}_{eg} = \int \Psi^*_e e \overrightarrow{r} \Psi _g d\overrightarrow{r}\,\!</math>
Since r, the operator, multiplies but not modifies the wave function, the r term can be rearranged in this way.
- <math>\overrightarrow{\mu}_{eg} = \int \Psi^*_e (\overrightarrow{r}) \Psi _g (\overrightarrow{r}) e\overrightarrow{r} d\overrightarrow{r}\,\!</math>
These wave functions will be key to the description of polarizabilities in molecular compounds. In this form the equation shows that in order to have large transition dipoles, it is necessary to have a reasonably good wave function overlap between the wave function of the initial state and the wave function of the final state. At the same time, it is also necessary to have that overlap for large values of r.
This means that if the two charges separate due to the polar attraction of the electric field of the light, it is clear that as the distance between two charges get larger, the dipole will become larger as well. Thus, the r value shows that dipole moment will be larger when the charges separate over a larger distance.
Polarizablity to polarization
Polarizability refers to a molecule and polarization refers to a material. When a molecule with a very large polarizability or material with a very large polarization is place in an electric field the electrons can move a large distance and delocalize a lot resulting in a separation of charges. Therefore, the larger the distance, the larger the state dipole, and the larger the transition dipole.
We will examine the behavior of individual molecule and then see what happens at the level of the material when many molecules come together.
Molecular Level
At the microscopic (molecular) level, a molecule that can have a permanent dipole moment , mu0 (permanent dipole) will have an induced dipole moment when it is exposed to electric field (or the electric field of the light). That induced dipole moment is proportional to the electric field an alpha (the polarizability) and the electric field. Thus, we can extend the analogy by acknowledging that the larger the alpha, the larger the polarizability, and the larger the induced dipole moment.
- <math>\overrightarrow{\mu} (induced) = \alpha \cdot \overrightarrow{E}\,\!</math>
where
- <math>\overrightarrow{\mu}\,\!</math> the dipole; a vector
- <math>\overrightarrow{E}\,\!</math> the electric field; a vector
- <math>\alpha\,\!</math> the polarizability is a tensor of rank 2
The electric field, the dipole moment, and induced dipole moment are vectors that have x, y, z components but alpha, the polarizability, is actually a tensor. It is a tensor because if an electric field is applied along x, not only can a dipole moment be generated along x but an induced dipole moment can also be generated along y or z. Therefore the induced dipole moment along axis i will depend on all the components of the field and these polarizability tensor components. So by measuring the induced dipole along mux, the x component of the field can also be observed and an alpha xx tensor component will be obtained.
- <math>\overrightarrow{\mu}_i = \sum_j \alpha_{ij} \overrightarrow{E}_j\,\!</math>
Those polarizability tensor components are a function of the wavelength.
- <math>\alpha_{ij} = f(\omega)\,\!</math>
Usually in the literature one talks about wavelengths and then shows the angular frequency, omega, not lambda. This may be confusing. The reason why the angular frequency is used is simply because the wavelength of the light refers to a very specific oscillation frequency of the electric field of the light.
Material Level
When looking at the macroscopic scale of the molecular material, one talks about the induced polarization of the material. Just like the microscopic scale, the induced polarization will be directly proportional to the electric field at the macroscopic scale.
- <math>\overrightarrow{P}(induced) = \Epsilon_0 \cdot \Chi_{el} \cdot \overrightarrow{E}\,\!</math>
where
- <math>\Epsilon_0\,\!</math> is the electric permittivity of a vacuum
- <math>\Chi_{el}\,\!</math> is the electric susceptibility of the material; a tensor
The displaced electric (D) field takes into account the external field, like the field due to the light and the polarization.
- <math>\overrightarrow{D} = \Epsilon_0 \overrightarrow{E} + \overrightarrow{P}\,\!</math>
- <math>\overrightarrow{D} = \Epsilon_0 \overrightarrow{E} + \Epsilon_0 \cdot \Chi_{el} \cdot \overrightarrow{E}\,\!</math>
- <math>\overrightarrow{D} = \Epsilon_0 \overrightarrow{E} (1+ \Chi)\,\!</math>
The displaced electric field can be expressed as the electric permittivity of the vacuum times the external field times (1 + χ). (1+χ) represents the electric susceptibility, which is an important characteristic of the material. It is also known as the dielectric constant. Dielectric constant is a function of frequency and wavelength and so it varies as a function of wavelength. Thus, it is constant to some extent. The dielectric constant is actually defined as the ratio of the electric permittivity of the medium itself over that of the vacuum.
- <math>\Epsilon_d = \frac {\Epsilon} {\Epsilon_0}\,\!</math> is the dialectric constant
Therefore, the dielectric constant has no dimension since it is a ratio of those two values. By substituting the ratio in the expression for the displaced electric field, a compact expression can be obtained that expresses the displaced electric field as simply the external field times the electric permittivity of the material.
- <math>\overrightarrow{D} = \Epsilon \overrightarrow{E}\,\!</math>
The permittivity and dielectric constant are a function of frequency (ω) or wavelenght (λ).
- <math>\Epsilon_{ij} (\omega) = 1 + \chi_{ij} (\omega)\,\!</math>
Relation between dielectric constant and refractive index
It is useful to keep in mind the simple relationship between the refractive index and the dielectric constant. Recall the definition of the speed of light, which is 1 over the square root of the electric permittivity of vacuum times the magnetic permeability of vacuum. When light enters a material (a medium), its speed becomes v, which is 1 over the square root of the product of the electric permittivity of that material or medium times the magnetic permittivity of that material or medium. In this case, mu here is the magnetic permittivity; not the dipole moment.
- <math>c = \frac { 1} {\sqrt{\Epsilon_0 \cdot \mu_o}}\,\!</math>
where
- <math>\Epsilon_0 \,\!</math>is the permittivity of vacuum
- <math>\mu_0 \,\!</math>is the magnetic constant or permeability of vacuum
The ratio of the speed of light in vacuum over that in the in the medium is the index of refraction.
- <math>\frac c v = n =\sqrt {\frac {\Epsilon \mu} {\Epsilon_0 {\mu_0}}}\,\!</math>
In the case of weakly magnetic materials μ = μ0
- <math>n(\omega)\approx \sqrt{\Epsilon_D (\omega)}\,\!</math>
The ratio of the speed of light in vacuum over that in the in the medium is the index of refraction.
- <math>n^2(\omega) \approx \Epsilon_D(\omega)\,\!</math>
For materials in which there is no magnetic activity, the magnetic permeability of the material is basically the magnetic permeability of the vacuum. Then the ratio of μ to μ0 will be close to one and thus the index of refraction will be nearly equal to the square root of the electric permittivity of the medium over that of the vacuum; this is the dielectric constant of the material. Often the interaction of the magnetic field with the light of the material is much smaller than the interaction of the electric field. Therefore, in many instances you can neglect the magnetic interactions and this expression would hold.
Eventually, this comes to an expression where the index of refraction squared corresponds to the dielectric constant. This is the connection between the index of refraction and the dielectric constant. It is important to remember that both the index of refraction and the dielectric constant depend on frequency. Also, often many people in the optics or photonics community casually quote the index of refraction for that material or the dielectric constant you will find that when the two numbers are compared, this expression appears to not hold true. This inconsistency is not due to an issue related to the magnetic material but it is simply because when people casually talk about the dielectric constant or index refraction, they are referring to the constant at very small frequency or in a static context where frequency tends to zero.
When people casually talk about the index refraction of the material, they usually mean optical frequencies. Optical frequencies are frequencies that correspond to the visible. Again, when one casually talks about index of refraction, one would imply optical frequencies where as in dielectric constants, one would imply very low frequencies.
Also, note that n, mu and Epsilon are also complex quantities because they may involve both dispersion effects and attenuation effects. As soon as there is absorption, then that becomes an imaginary component to the expression. Thus, all of those are complex numbers.
| Return to Quantum Mechanical and Perturbation Theory Menu | Next Topic |