Metricon Prism Coupler
| Return to Research Tool Menu |
Background
Optical characterization of thin films can be easily and accurately performed through the use of a prism coupler, specifically the Metricon Model 2010 prism coupler (Figure 1). The prism coupler is able to make its highly accurate measurements (±.0002) by directing a laser of a specific wavelength to a prism of a high refractive index, which is coupled with a sample with a pressure ranging from 20psi to about 40psi. Good coupling to the film is indicated by the appearance of a coupling or “wet” spot at the interface between the prism and the film, indicating the frustration of total internal reflection at that point. The prism, sample, and photodetector are mounted on a stage that rotates and varies the angle at which the laser enters the prism thus allowing the waveguide modes of the film
to be determined. When three or more modes are found the prism coupler is able to calculate the index of refraction, substrate film thickness and the standard deviations of these quantities. Measurements are generally repeated at different spots on the sample until the standard deviation of the sample thickness is determined to be less than 2% as determined by the Metricon’s fitting routines. The refractive index can be measured at five different wavelengths, 532nm, 632.8nm, 830nm, 1300nm, and 1550nm to enable accurate determination of the refractive index dispersion. The sample films involved were formulated and fabricated using spin coating, a technique that is commonly used in the semiconductor industry. In this mode of operation ideal film thicknesses are ordinarily in the range of 3-5 μm. Both the TE index and TM index can be measured at each wavelength through the insertion of actuator driven waveplates. The TE index is the refractive index for waveguide modes polarized parallel to the surface of the film, while TM modes are polarized normal to the surface of the film.
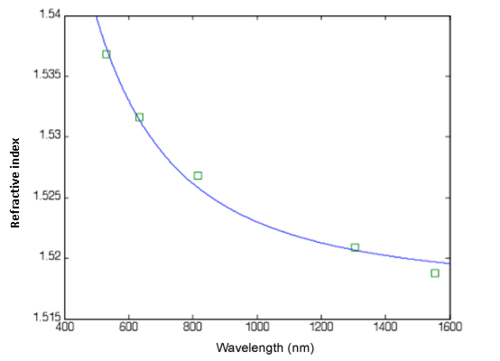
The wavelength dependent refractive index data obtained can then be analyzed and fit to an appropriate dispersion relationship, such as the Cauchy or the Sellmeier. A Cauchy fit to data obtained for a low-loss organically modified sol-gel material is shown in Figure 2, with the Cauchy formula given by
- <math>
n(\lambda) = A + \frac {B} {\lambda^2} + \frac {C} {\lambda^4}\,\!</math>
This formula is generally applicable to materials far from any significant absorption bands. The error bars in Figure 2 are basically the size of the data point, evidencing the high precision of the Metricon measurement. The fit is quite good with some small disagreement at 1550nm.
Contributed by Robert A. Norwood College of Optical Sciences University of Arizona