Director – Degrees of Order in Liquid Crystals
| Previous Topic | Return to Liquid Crystal Menu | Next Topic |
The optical properties of a molecule only are useful when they translate into optical properties of a bulk material. The order of liquid crystals in material is critical to their functionality.
Degrees of Order in Liquid Crystals
There of typically three types of order that characterize liquid crystals: I) orientational order, ii) positional order and iii) bond orientational order The degree of orientation and positional order in LC phases can vary and depending upon this degree the material may be more liquid-like or more crystal-like. It takes more or less energy to change the orientation of various liquid crystals.
In general, based on the enthalpy of the transitions, it is concluded that LCs are more liquid-like since the greatest enthalpy of transition occurs upon going from the crystal to the first LC phase. You tend lose most of the order going from crystalline or liquid crystal state.
For a given material it is possible for there to be several discrete LC phases.
As a function of temperature, it is therefore possible to see several transitions with increasing temperature upon a transition the newly created phase has increased disorder.
The Director
Rod like liquid crystals are generally oriented with their moments of inertia roughly aligned along an axis that is called the director.
The smaller the average angle of displacement of the moment of inertia from the director, the more ordered the liquid crystal is. The order parameter is given by
- <math>S = \left \langle \frac{3 \cos^2 \theta-1}{2} \right \rangle </math>
Where:
- <math>\theta\,\!</math> is the angle between any molecule and the average director
When θ is zero there is a very high degree of organization order. For most liquid crystals the orientational order parameter varies between .3 (not very ordered) and .9 (very ordered).
Thus, when θ is 0° for all the molecules, the orientation parameter is one, which is the case for a crystal in the space group P1 for example. When θ is 57° the orientational order is by this definition 0.
Order as a function of Temperature
The orientational order decreases with increasing temperature and then goes to zero (isotropic) at the clearing temperature (the temperature for the transition to an isotropic phase). At higher temperatures the molecules have more thermal energy and they can sample more angles of space.
Positional order is the degree to which the position of an average molecule or groups of molecules exhibit translational symmetry.
In liquid crystal there are cohesive forces between the molecules that makes them try to orient in one direction. At the same time the temperature is causing entropy in the system. So the interplay between cohesive forces and thermal entropy that enable liquid crystal states and determine the order parameter with respect to temperature.
Enthalpy of Phase Transitions
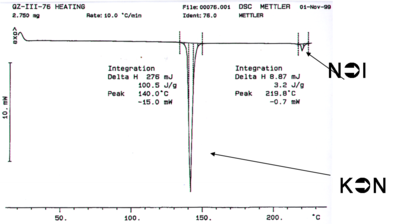
This liquid crystal was made in the Marder lab. The differential scanning calorimetry (DSC) measures the amount of the amount of energy that must be added to a sample to change the temperature 1 degree C. Differential scanning calorimetry can be used to characterize the temperature at which phase transitions occur, as can optical microscopy. If a system has an enthalpy change there can be an absorption of energy without a change in temperature. For example when water goes from ice to liquid state a lot of energy is added without a change in temperature. This is expressed in the DSC in the form of a heat flow without temperature change. If you know the precise amount of material and then calculate the area under the curve you can calculate the heat delivered and therefore the enthalpy of a transition.
The first transition is the crystal to nematic transition (K→N), the second dip is the nematic to isotropic transition (N→I). The enthalpy for the liquid crystal to isotropic transition is substantially lower than the crystalline to nematic transition. If the reverse process is run in the opposite direction the same curve result possibly with some hysteresis (displacement of the lines) if the system is not run sufficiently slowly. If these are true liquid crystals, and there is no decomposition, it should be possible to cycle back and forth between crystalline, liquid crystalline and isotropic states.
See Wikipedia on Differential scanning calorimetry
| Previous Topic | Return to Liquid Crystal Menu | Next Topic |