Electrochemical Impedence Spectroscopy EIS
Impedance Basics
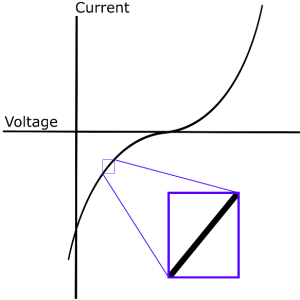
Electrochemical Impedance Spectroscopy (EIS) is a frequency domain measurement made by applying a sinusoidal perturbation, often a voltage, to a system. The impedance at a given frequency is related to processes occurring at timescales of the inverse frequency (e.g. f=10 Hz, t=0.1 s). Although many other electrochemical measurements focus on driving a system far from equilibrium with potential sweeps or steps, such as cyclic voltammetry or chronoamperometry, EIS uses small perturbations. These small departures from equilibrium are assumed to have a linear response (Fig. 1), thus greatly simplifying the frequency analysis; however, linearization of physical models can lead to indistinguishable cases, as will be discussed in the Nonlinear EIS (NLEIS) section. Furthermore, operating conditions for relevant devices (e.g. batteries and fuel cells) are often far from equilibrium and exhibit nonlinear behavior. Practically speaking, EIS is performed by sweeping through a wide range of frequencies at a single perturbation amplitude. As instrumentation has improved over the last several decades, frequencies ranging from 10-4 to 108 Hz are attainable, thus allowing for the study of both fast kinetic and slow transport process1.
Broadly defined, impedance is the opposition of an electrical system to the flow of electric current and carries units of Ohms, Ω. It reduces to resistance under the following conditions: (1) there is no phase shift in current under an applied potential, and vice versa (2) all potentials and currents can be used (i.e. there is no saturation potential) (3) the impedance is not a function of frequency2. Under these conditions, the well-known Ohm’s Law applies:
(1) V=IR or R=V/I
Where V is the voltage in V, I is the current in A, and R is the resistance in Ω. However, in EIS both V and I are time dependent, sinusoidal functions. A single frequency potential input with amplitude, Vo, and radial frequency, ω, can be expressed as:
(2) V(t)=V_o cos(ωt)
Note that EIS data is usually discussed in terms of linear frequency, f, with units of Hz. The conversion is ω=2πf. In a real system, the current output will have some phase shift, φ, and an amplitude, Io, expressed as:
(3) <math display="inline">\[V_{\left (t \right )}=V_{o}\cos \left ( \omega T+\varphi \right )\]
</math>
For a generalized expression of impedance, Z, the previously stated conditions for Ohm’s law are relaxed, and the time-dependent expressions for V and I are substituted into Eq. 1:
(4) Z=(V(t))/(I(t))=(V_o cos(ωt))/(I_o cos(ωt+φ))=Z_o (cos(ωt))/(cos(ωt+φ))
Again, we see that if the system exhibits no phase shift (φ=0), Eq. 4 reduces to Ohm’s Law3.
Equivalent Electrical Circuit Elements
Interpretation of EIS data has traditionally relied on models containing Equivalent Electrical Circuit (EEC) elements, where spectra are represented as combinations of circuit elements, such as resistors, capacitors, and inductors. These elements are then attributed to physical processes in the system (e.g. double layer capacitance, charge transfer resistance, etc.). Although this method may be appropriate for simple systems with well-defined physics, it may not be able to discern the differences between proposed local processes, such as reaction mechanisms. In any case, the impedance relations for these elements are given below.
(5) Z_resistor=R
(6) Z_capacitor=1/jωC
(7) Z_inductor=jωL
Where C is capacitance in F and L is inductance in H. Note that j=√-1, contrary to IUPAC convention so as to not be confused with current. Other elements without analogy to electrical circuits have also been used to represent EIS behavior not captured by the three included here (e.g. Warburg Impedance and constant phase element). For details regarding the derivation of Eqs. 5-7 and explanation of other EEC elements please see 3.
In developing EEC models for an EIS spectrum, impedance relations are treated with the same rules as resistors in circuit combinations. Graphical and mathematical representations for a circuit comprised of elements in series and parallel are given in Figs. 2 and 3, respectively.
〖 Z〗_eq=Z_1+Z_2+⋯+Z_n (b) Fig. 2 (a) Graphical and (b) mathematical representation of circuit elements in series.
Z_eq=Z_1+Z_2+⋯+Z_n
(b)
Fig. 3 (a) Graphical and (b) mathematical representation of circuit elements in parallel.
EEC Model Example
As an example, let us examine a circuit composed of a resistor element, Rs, followed by a resistor, Rr, and a capacitor, Cdl, in parallel. Graphical and mathematical representations of this circuit are given in Figure 4.
Z_eq=R_s+1/(1/R_r +jωC_dl )=R_s+R_r/(1+jωR_r C_dl )
(b) Fig. 4 (a) Graphical and (b) mathematical representations of an RRC circuit, or Simplified Randles cell. This circuit is known as the Simplified Randles Cell, which can be used to model processes with a single electrochemical reaction, such as iron corrosion in an anaerobic aqueous environment. Further details on relating this EEC model to a kinetic model can be found in Example 10.1 of Ref. 3. If we further manipulate the equation in Fig. 4(b), we can separate the expression into its real and imaginary parts: (8) Z_Re=R_s+R_r/(1+ω^2 〖R_r〗^2 〖C_dl〗^2 ) Z_Im=(-jωC_dl 〖R_r〗^2)/(1+ω^2 〖R_r〗^2 〖C_dl〗^2 )
Nyquist Plots
At this point it is useful to discuss the most common ways to present EIS spectra, and how to glean useful information from them. First is the Complex-Impedance Plane representation, or Nyquist Plot, in which the data from each frequency point is plotted by the imaginary part on the ordinate and the real part on the abscissa. It is a common convention in the electrochemistry community to plot -ZIm (also found as -Z’’ or -Zj’’) on the y-axis so the data fit into the first quadrant of a graph. Although this type of plot is valuable for identifying how many characteristic features are exhibited by a system, all frequency information is inherently lost. To compensate, one should always annotate the frequencies of crucial data points like high and low real axis intercepts, and the characteristic frequency of an arc, ωc. This characteristic frequency is that which exhibits a maximum in -ZIm for a feature. An example of a Nyquist plot for the circuit in Fig. 4(a) with values Rs=47 Ω, Rr=467 Ω, and Cdl=860nF is shown in Figure 5.
Fig 5. Nyquist plot of a Simple Randles Cell with values Rs=47 Ω, Rr=467 Ω, and Cdl=860nF The values listed above were known a priori since the EIS spectrum was collected from an actual circuit containing these elements; however, these values can be obtained easily with a model fitting program or a known EEC model. The high-frequency intercept yields Rs, the value of frequency-independent contributions, most commonly the ohmic resistance of the electrolyte. The low-frequency intercept gives Rs+Rr, and, therefore Rr, after subtracting Rs. This is the characteristic impedance of the feature. The characteristic capacitance of this feature is found using Rr and ωc with the following formula: (9) C=1/(R_r ω_c ) Furthermore, the shape of features, such as multiple semicircles or a 45˚ low-frequency tail, gives possible insight into the governing kinetic or transport phenomena. Further details on analyzing Nyquist plots can be found in Ref. 2 or Chapter 16 Ref. 3.
Bode Plots
Another common representation is the Bode Plot, in which the impedance magnitude and phase angle are plotted against frequency. The magnitude and phase angle are given by Eqs. 10 and 11, respectively.
(10) |Z|=√(〖Z_Re〗^2+〖Z_Im〗^2 )
(11) φ=〖tan〗^(-1) (Z_Im/Z_Re )
Due to the large range of values often encountered in |Z| and f, they are plotted on log scales for easier examination of small values. Again, the high-frequency limit of |Z| yields Rs, and the low-frequency limit yields Rs+Rr. The slope of the transition region between the two asymptotic limits reveals the power of the frequency dependence in the imaginary part (-1 in our example). The frequency at which φ=-45˚ should give the characteristic frequency of the feature; however, in our example we see it crosses this line at both f=500 Hz and f=3,300 Hz. This error is due to the dominance of Rs at high frequencies, which obscures the behavior of the process responsible for the EIS feature. As such, Rs, or an estimate of Rs, should be subtracted from the real and imaginary parts of the entire data set.
Fig. 6 Bode Plot of a Simple Randles Cell with values Rs=47 Ω, Rr=467 Ω, and Cdl=860nF
As a final note on EIS, it is commonplace to find area-specific impedance data, which is achieved by multiplying the real and imaginary parts of the impedance by the electrode cross-sectional area.
Nonlinear EIS
NLEIS is essentially an extension of EIS which operates on many of the same principles. The key difference is the use of perturbation amplitudes which produce responses larger than appropriate for linear treatment. This allows for direct investigation of nonlinear system behavior. These nonlinearities are analyzed by collecting response signals at integer multiples of the input frequency, ω. Additionally, it is performed using current perturbations rather than voltage perturbations often used in EIS.
Higher Harmonic Analysis
Before addressing how NLEIS spectra are reported and interpreted, it is useful to understand how higher order harmonics are extracted from a complex signal. First, recall that a steady periodic function can be expressed as a Fourier series4.
(12) f(t)=∑_(n=1)^∞▒〖(a_n 〗 cos(nωt)+b_n sin(nωt))
Or, using trigonometric identities for complex numbers:
(13) f(t)=∑_(n=1)^∞▒〖(c ̃_n 〗 exp(jnωt)+c ̃_(-n) exp(-jnωt))
Where c ̃_n=(a_n+b_n)/2 and c ̃_(-n)=(a_n-b_n)/2. Now, when this is applied to the voltage response from a current perturbation with frequency ω ̃ we find:
(14) V(t;ω ̃,i ̃ )=1/2 ∑_(k=1)^∞▒〖(V ̂_k (ω ̃,i ̃)〗 exp(kjω ̃t)+V ̂_(-k) (ω ̃,i ̃)exp(-kjω ̃t))
Where V ̂_(∓k)=V ̂'_k±jV ̂_k are complex Fourier coefficients for the kth harmonic. As with impedance data, a prime indicates the real part and a double prime indicates the imaginary part. The nonlinear dependence of the Fourier coefficients is then expressed as a power series:
(15) V ̂_k (ω ̃,i ̃ )=∑_(r=1)^∞▒〖α^(k+2r-2) V ̂_(k+2r-2) (ω ̃)〗
Where r is the order of nonlinear contribution to the kth order harmonic. For example, with k=r=1 we have V ̂_1,1, which is simply the linear response. These coefficients are found by fitting data from multiple amplitude perturbations at each desired frequency5. These amplitudes should be chosen to elicit purely linear behavior at the lover limit, and behavior that is one term higher than the desired power series order (e.g. 5th harmonic if truncating the power series at k=3). NLEIS Representation Once these Fourier coefficients are fit, they can be presented in a Complex-Plane representation, similar to Nyquist plots. An NLEIS spectrum of La0.6Sr0.4Co0.2Fe0.8O3-δ (LSFC-6428) at 600 ˚C under various PO2 environments is provided as an example in Figure 76. In this case, all harmonic data has been nondimensionalized and normalized with respect to the maximum absolute value of the imaginary component of the linear response. Other workers have chosen to report harmonic data in dimensional, non-normalized form6. Unfortunately, at this time there is no way to interpret higher harmonic data without support from a physical model like there is in the linear EIS community (e.g. low-frequency 45˚ tail indicates semi-infinite diffusion).
Fig. 7 2nd harmonic spectra of a porous LSCF-6428 electrode at 600 ˚C. Lines extending from origin are phasor lines intersecting Uk,k at 1/k ω ̃_c; 1/2 ω ̃_c in this case6.
NLEIS Interpretation
Interpretation of NLEIS spectra instead relies on proposing physical models for phenomena in an electrochemical system and calculating harmonic spectra thereof. In fact, it is through this framework that NLEIS can verify, or at least eliminate, proposed mechanisms which may be indistinguishable in linear EIS. To extend current knowledge of oxygen reduction behavior on porous LSCF-6428 electrodes, Tim Geary performed extensive NLEIS studies. He performed experiments under several temperatures and PO2 relevant for intermediate temperature SOFC operation and evaluated several modeling scenarios. Details regarding the modeling scenarios can be found in Ref. 6. As an example, Figure 8 compares the results between models assuming oxygen chemisorption and dissociative adsorption limited rate laws. Both models assume the surface behaves identically to the bulk, and bulk transport is the only pathway for oxygen vacancies. Although neither scenario accurately captured the electrode behavior, it did indicate that a more complex framework of surface thermodynamics was merited.
Fig. 8 2nd Harmonic spectra of a porous LSCF-6428 electrode at 650 ˚C. Lines extending from origin are phasor lines intersecting Uk,k at 1/k ω ̃_c; 1/2 ω ̃_c in this case6.
References:
1. Bard, A. J. & Faulkner, L. R. Electrochemical Methods: Fundamentals and Applications. (John Wiley & Sons, Inc., 2001).
2. Basics of EIS: Electrochemical Research-Impedance. Available at: https://www.gamry.com/application-notes/EIS/basics-of-electrochemical-impedance-spectroscopy/. (Accessed: 15th June 2017)
3. Orazem, M. E. & Tribollet, B. Electrochemical Impedance Spectroscopy. (John Wiley & Sons, Inc., 2008).
4. Wilson, J. R., Schwartz, D. T. & Adler, S. B. Nonlinear electrochemical impedance spectroscopy for solid oxide fuel cell cathode materials. Electrochimica Acta 51, 1389–1402 (2006).
5. Murbach, M. D. & Schwartz, D. T. Extending Newman’s Pseudo-Two-Dimensional Lithium-Ion Battery Impedance Simulation Approach to Include the Nonlinear Harmonic Response. J. Electrochem. Soc. 164, E3311–E3320 (2017).
6. Geary, T. C. Lanthanum Ferrite-Based Mixed-Conducting Electrodes for Solid Oxide Fuel Cells and Electrolyzers. (University of Washington, 2014).